Single Cell Genomics
Single cell RNA sequencing (scRNAseq) has emerged as a powerful tool in genomics. While previous bulk RNAseq measures average gene expression levels across many cells in a sample with potential heterogeneity, scRNAseq can measure gene expression at the single cell level. The high resolution of scRNAseq has thus far transformed the genomics field: scRNAseq has been applied to classify novel cell subtypes and cellular states, quantify progressive gene expression, perform spatial mapping, identify differentially expressed genes, and investigate the genetic basis of gene expression variation. Compared with the fast development of scRNAseq technology, methods development for scRNAseq data has fallen behind. Analyzing scRNAseq data faces important statistical and computational challenges that arise from the complexities and unique features of scRNAseq data. We developed several methods that combat these challenges: 1) scPLS: a method to control for confounding effects for accurate downstream analysis; 2) VIPER: the only method to preserve gene expression variability across cells after accounting for drop-out and imputing zero values. We are now working on projects including integrating scRNAseq across samples and transfer learning with public available scRNAseq datasets.
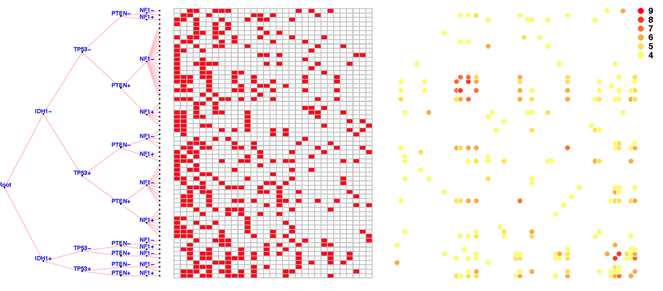
By expressing prior distributions as general stochastic processes, nonparametric Bayesian methods provide a flexible way to incorporate prior knowledge and constrain the latent structure in statistical inference. The Indian buffet process (IBP) is such an approach that can be used to define a prior distribution on infinite binary features, where the exchangeability among subjects is assumed. The Phylogenetic Indian buffet process (pIBP), a derivative of IBP, enables the modeling of non-exchangeability among subjects through a stochastic process on a rooted tree, which is similar to that used in phylogenetics, to describe relationships among the subjects.
In this paper, we study both theoretical properties and practical usefulness of IBP and pIBP for binary factor models. For theoretical analysis, we established the posterior convergence rates for both IBP and pIBP and substantiated the theoretical results through simulation studies. As for application, we apply IBP and pIBP to data arising in the field of cancer genomics where we incorporate somatic mutations as prior information into gene expression data to study tumor heterogeneities. The results suggest that incorporating heterogeneity among subjects through pIBP may lead to better understanding of molecular mechanisms under tumor genesis and progression.
Related reference:
Miller, K. T., Griffiths, T., and Jordan, M. I. (2012), “The phylogenetic indian buffet process: A non-exchangeable nonparametric prior for latent features,” arXiv:1206.3279.
Griffiths, T. L., and Ghahramani, Z. (2011), “The indian buffet process: An introduction and review,” Journal of Machine Learning Research, 12, 1185–1224.
In this paper, we study both theoretical properties and practical usefulness of IBP and pIBP for binary factor models. For theoretical analysis, we established the posterior convergence rates for both IBP and pIBP and substantiated the theoretical results through simulation studies. As for application, we apply IBP and pIBP to data arising in the field of cancer genomics where we incorporate somatic mutations as prior information into gene expression data to study tumor heterogeneities. The results suggest that incorporating heterogeneity among subjects through pIBP may lead to better understanding of molecular mechanisms under tumor genesis and progression.
Related reference:
Miller, K. T., Griffiths, T., and Jordan, M. I. (2012), “The phylogenetic indian buffet process: A non-exchangeable nonparametric prior for latent features,” arXiv:1206.3279.
Griffiths, T. L., and Ghahramani, Z. (2011), “The indian buffet process: An introduction and review,” Journal of Machine Learning Research, 12, 1185–1224.
2. Change Point Analysis of Histone Modifications Reveals Epigenetic Blocks with Distinct Regulatory Activity and Biological Functions
(Work with Haifan Lin and Hongyu Zhao) [paper]
(Work with Haifan Lin and Hongyu Zhao) [paper]
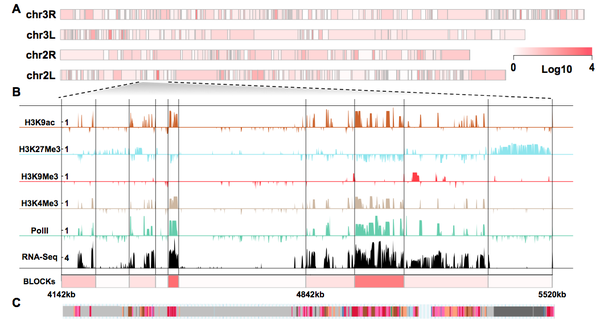
Histone modification is a vital epigenetic mechanism for transcriptional control in eukaryotes. High- throughput techniques have enabled whole-genome analysis of histone modifications in recent years. However, most studies assume one combination of histone modification invariantly translates to one transcriptional output regardless of local chromatin environment. In this study we hypothesize that, the genome is organized into local domains that manifest similar enrichment pattern of histone modification, which leads to orchestrated regulation of expression of genes with relevant biological functions.
We propose a multivariate Bayesian Change Point (BCP) model to segment the Drosophila melanogaster genome into consecutive blocks on the basis of combinatorial patterns of histone marks. We find that these blocks, although inferred merely from histone modifications, reveal strong relevance with transcriptional events, and binding profiles of a broad panel of chromatin proteins. At least 60% of the inferred blocks are enriched for similar biological functions and display a high degree of co-expression during development. Our results suggest that these blocks represent genomic domains containing functionally relevant genes with coordinated regulation, and they reveal epigenetic organizational units resembling “operons” in prokaryotic genomes.
Related reference:
Barry, D. and Hartigan, J. A. (1993). "A Bayesian Analysis for Change Point Problems". Journal of the American Statistical Association, 88, 309–319.
Barry, D. and Hartigan, J. A. (1992). "Product Partition Models for Change Point Problems". The Annals of Statistics, 20, 260–279.
We propose a multivariate Bayesian Change Point (BCP) model to segment the Drosophila melanogaster genome into consecutive blocks on the basis of combinatorial patterns of histone marks. We find that these blocks, although inferred merely from histone modifications, reveal strong relevance with transcriptional events, and binding profiles of a broad panel of chromatin proteins. At least 60% of the inferred blocks are enriched for similar biological functions and display a high degree of co-expression during development. Our results suggest that these blocks represent genomic domains containing functionally relevant genes with coordinated regulation, and they reveal epigenetic organizational units resembling “operons” in prokaryotic genomes.
Related reference:
Barry, D. and Hartigan, J. A. (1993). "A Bayesian Analysis for Change Point Problems". Journal of the American Statistical Association, 88, 309–319.
Barry, D. and Hartigan, J. A. (1992). "Product Partition Models for Change Point Problems". The Annals of Statistics, 20, 260–279.
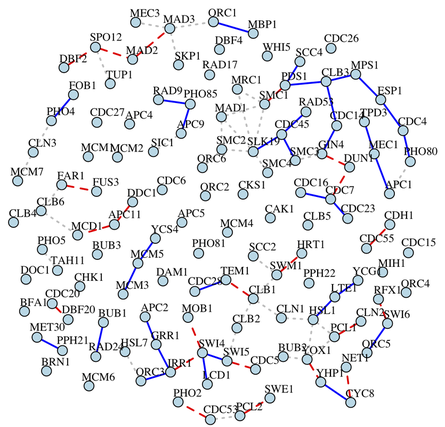
3. Conditional Gaussian Graphical Model for eQTL Study
(With Zhao Ren, Hongyu Zhao, Harrison Zhou) [paper]
Expression Quantitative Trait Loci (eQTL) mapping is a powerful approach to detecting transcriptional regulatory relationships at the genome scale. Using high-throughput data gathered through microarray or RNA-Seq experiments, eQTL mapping enables the analysis of thousands of expression traits simultaneously, and shed lights on molecular mechanisms for expression regulations. . Analogous to gaussian graphical models used to infer the genetic regulatory network from gene expression data, conditional gaussian graphical models (cGGM) have been proposed to infer the regulatory network from eQTL data. By identifying the conditional dependency among a set of genes after removing the effects from genetic variants, the graph inferred from cGGM may better reflect gene regulation at the expression level. recently proposed a tuning-free two-stage approach ANTAC (Asymptotically Normal estimation with Thresholding after Adjusting Covariates) for cGGM inference when the precision matrix is sufficiently sparse. For eQTL data, this approach not only reflects the strength of the regulatory relationships among genes through partial correlations but also provides P-values to reflect the statistical significance of the detected relationships.
See more information about this project in the software page.
Related reference:
Cai, T. T., Li, H., Liu, W., & Xie, J. (2013), “Covariate-adjusted precision matrix estimation with an application in genetical genomics,” Biometrika, 100(1), 139–156.
Li, B., Chun, H., & Zhao, H. (2012), “Sparse estimation of conditional graphical models with ap- plication to gene networks,” Journal of the American Statistical Association, 107(497), 152–167.
Yin, J., & Li, H. (2011), “A sparse conditional Gaussian graphical model for analysis of genetical genomics data,” The annals of applied statistics, 5(4), 2630.
See more information about this project in the software page.
Related reference:
Cai, T. T., Li, H., Liu, W., & Xie, J. (2013), “Covariate-adjusted precision matrix estimation with an application in genetical genomics,” Biometrika, 100(1), 139–156.
Li, B., Chun, H., & Zhao, H. (2012), “Sparse estimation of conditional graphical models with ap- plication to gene networks,” Journal of the American Statistical Association, 107(497), 152–167.
Yin, J., & Li, H. (2011), “A sparse conditional Gaussian graphical model for analysis of genetical genomics data,” The annals of applied statistics, 5(4), 2630.
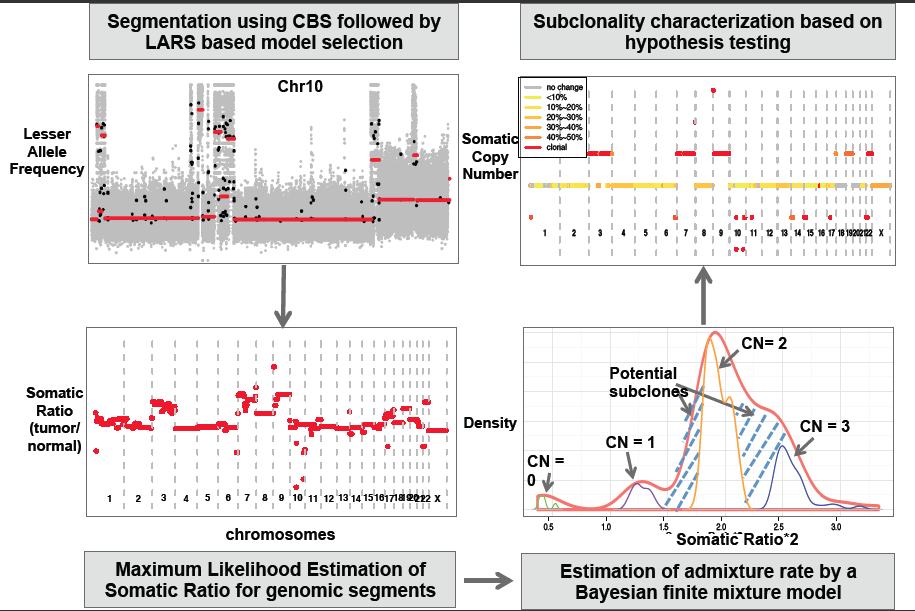
4. SomatiCA: Identifying, Characterizing and Quantifying Somatic Copy Number
Aberrations from Cancer Genome Sequencing Data
(With Murat Gunel and Hongyu Zhao)
We present SomatiCA, a novel framework that is capable of identifying, characterizing and quantifying SCNAs from cancer genome sequencing. By directly accounting for tumor purity and subclonality, SomatiCA was specially developed to analyze tumor samples with contamination and/or heterogeneity. First, SomatiCA segments the genome and identifies candidate CNAs utilizing both read depths (RD) and lesser allele frequencies (LAF) from mapped reads. Second, SomatiCA estimates the admixture rate from the relative copy-number ratios of a tumor-normal pair by a Bayesian finite mixture model, which has high tolerance on contamination from normal cells. Finally, SomatiCA quantifies somatic copy-number and subclonality for each genomic segment to guide its characterization. Results from SomatiCA can be further integrated with SNVs from the same sequencing experiment to gain a better understanding of tumor evolution.
See more information about this project in the software page.
See more information about this project in the software page.